Notes on Regression - Projection | Quasilinear Musings

This is one of my favourite ways of establishing the traditional OLS formula. I remember being totally amazed when I first found out how to derive the OLS formula in a class on linear algebra. Understanding regression through the perspective of projections also shows the connection between the least squares method and linear algebra. It also gives a nice way of visualising the geometry of the OLS technique.

This set of notes is largely inspired by a section in Gilbert Strang's course on linear algebra.^[My two favourite sources covering the basics of linear algebra are Hefferon's linear algebra, a free textbook, and Gilbert Strang's course mentioned above. Hefferon provides a very clear treatment on the more theoretical aspects of the subject, while the latter highlights the many possibilities and applications that one can do with it.] I will use the same terminology as in the previous post.

Recall the standard regression model and observe the similarities with the commonly used expression in linear algebra written below:

\begin{aligned} \mathbf{y} &= \mathbf{X}\mathbf{\beta} \\ b &= Ax \end{aligned}

Thus, the OLS regression can be motivated as a means of finding the projection of $\mathbf{y}$ on the space span by $\mathbf{X}$ .^[The span of the vectors in $\mathbf{X}$ (column space) is the set of all vectors in $R^{n}$ that can be written as linear combinations of the columns of $\mathbf{X}$ ] Or to put it another way, we want to find the vector $\beta$ that would be the closest to $\mathbf{y}$ .

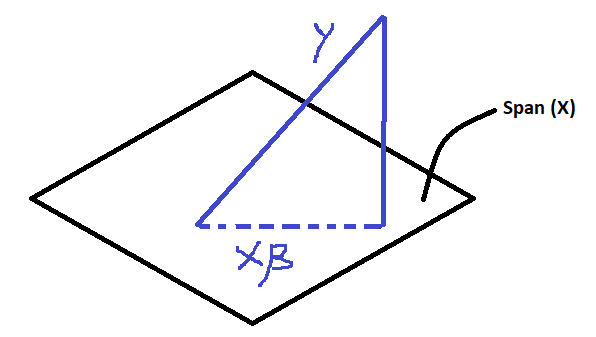
Notice that $(\mathbf{y} - \mathbf{X}\beta)$ is orthogonal to $Span (\mathbf{X})$ i.e. it is in the left nullspace of $\mathbf{X}$ . By the definition of nullspace:

\begin{aligned} \mathbf{X}'(\mathbf{y} -\mathbf{X}\hat{\beta}) &= 0 \\ \mathbf{X}'\mathbf{y} &= \mathbf{X}'\mathbf{X}\hat{\beta} \\ \hat{\beta} &= (\mathbf{X}'\mathbf{X})^{-1}\mathbf{X}'\mathbf{y} \end{aligned}

Notes:

$\mathbf{X}\hat{\beta} = \mathbf{X}(\mathbf{X}'\mathbf{X})^{-1}\mathbf{X}'\mathbf{y} = P_{x}$ is also known as the orthogonal projection matrix. The matrix is $n~\times~n$ dimension. As given by its name, for any vector $b \in R^{n}$ , $P_{x}b \in Span(X)$ .
$\mathbf{y} - \mathbf{X}\hat{\beta}$ is simply the vector of residuals and can be written in the following form:

\begin{aligned} \hat{u} &= \mathbf{y} - \mathbf{X}\hat{\beta} \\ &= \mathbf{y} - P_{x}\mathbf{y} \\ &= (I_{n} - P_{x})\mathbf{y} \\ &= M_{x}\mathbf{y} \end{aligned}

$M_{x}$ is the projection onto the space orthogonal to $Span(X)$ .

The projection matrices have the following four properties: $P_{x} + M_{x} = I_{n}$ , Symmetry ( $A'=A$ ), Idempotent ( $AA=A$ ), Orthogonal ( $P_{x}M_{x} = 0$ ).

Additional Comments:

The idea of seeing fitted values and residuals in terms of projections and orthogonal spaces have further applications in econometrics. See for example the derivation of the partitioned regression formula.
As a fun exercise one can try to derive the OLS formula for a weighted regression $\mathbf{W}\mathbf{X}\beta = \mathbf{W}\mathbf{y}$ where $\mathbf{W}$ is an $n \times n$ matrix of weights using the same idea.